Medical Diagnosis Solution

The correct answer is just below 2%.

Before explaning why, it is worth mentioning the implications of this result. The medical experts believe that the positive test result implies the patient is likely to have the disease. Most members of the public would believe the same.  But both the experts and the public are completely wrong. The positive test result certainly increases our belief that the patient has the disease, but the probability is still extremely small.  What happens in practice (and this is a known problem, for example, for breast cancer screening tests) is that the misunderstanding about the true probability leads not only to unncessary anguish by the patient but also to further unnecessary tests and even unnecessary surgery.  

This very common and serious fallacy is known as the 'base-rate neglect' fallacy - people neglect to take into consideration the very low probability (of having the disease) that you start from.

An informal way of explaining this result is to think of a population of 10,000 people. We would expect just 10 people in this population to have the disease. But if you test everybody in the population then, in addition to the 10 people who do have the disease, another 500 (that's 5% of the 10,000) will be wrongly diagnosed as having it. In other words only about 2% of the people diagnosed positive (i.e. 10 out of the 510) actually have the disease. When people give a high answer like 95% they are ignoring the very low probability of having the disease. In comparison, the probability of a false positive test is relatively high.

A formal explanation (shown below) requires an understanding of Bayesian reasoning. If you prefer not to look at the 'maths' then you can simply run this model using the AgenaRisk software.



For those who can stomach the Maths (it really is not that hard)

Let A be the event 'person has the disease'

let B be the event 'positive test'.

We wish to calculate the probability of A given B, which is written p(A|B).

By Bayes Theorem this is:

 

 

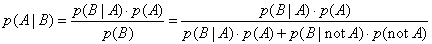
Now, we know the following:

p(A)=0.001

p(not A)=0.999

p(B| not A) = 0.05

p(B|A) = 1

Hence:

 
 

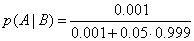
which is equal to 0.1963