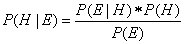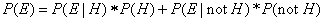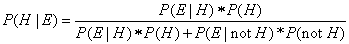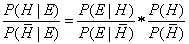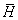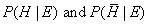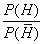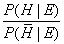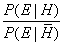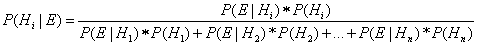Bayes Theorem
You should read the lay introduction here first (which talks about Bayes in the context of legal evidence) if you are not comfortable with basic probability and maths.
We start with some hypothesis (let's call it
H). In
the legal context this is usually the statement "Defendant is innocent". In
this case the hypothesis is either true or false (that is not always
the case but you do not need to assume anything else in order to
understand Bayes Theorem).
We must have what we call a prior belief
about H
(most mathematicians and statisticians at this point already unnecessarily
complicate things by talking about a person's belief being conditional
on their state of knowledge of the world and to understand what they
mean here you already have to understand the notion of 'conditional
probability', which is actually what Bayes theorem is really all about - so it all
gets a bit circular).
The prior belief about H is written as P(H) to stand for "the
probability of H". So, in the legal example this is your (initial) belief about the probability the defendant is
innocent.
What now happens is that you start to find out evidence E. For example, E might be the statement "a blood sample of the criminal found at the
scene matches the blood type of the defendent". The question that Bayes Theorem
answers precisely is
the following :
"what is the revised (posterior) belief about the
defendent being inncocent given the evidence". This revised belief is written as P(H | E) meaning "the probability of the
hypothesis H given the evidence E".
It turns out that, whereas answering this question directly is normally
difficult, it is easier to
answer the following question:
"what
is the probability of seeing the
evidence given that the defendent is innocent." This is written as P(E | H) meaning "the probability of the evidence
E given the hypothesis H". It is also referred to as the 'likelihood''.
Pictorially we can represent this question 3 as:
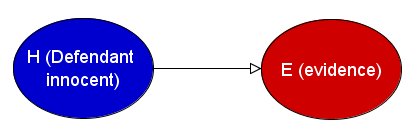
So, if the evidence was the matching blood type and if that blood
type is
found in 1 in every 10 people, then P(E | H) is clearly equal to 0.1.
Bayes Theorem is simply a way of calculating the thing we are really
interested in knowing, namely P(H | E), in terms of what we
started with, namely P(H) and what we can find out directly, namely P(E
| H).
Bayes Theorem is the following formula
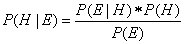
The denominator in this formula, P(E), is the probability of the
evidence irrespective of our knowledge about H. Since H can be either
true or false, it is also the case that
(for an explanation of this see here).
Hence the 'full' version of Bayes Theorem is the following formula
In our example suppose we start with P(H)=0.4, then, since we know P(E | H) = 0.1 it follows that the numerator in Bayes Theorem is 0.04.
For the denominator we also need to know P( not H) and P(E | not H).
Now since P(H) = 0.4 we must have P( not H) = 0.6 ("not H" is the
assertion "defendent is not innocent" or equivalently "the defendant is
guilty").
That only leaves the term P(E | not H). In our example ths is the
probability that the defendent's blood type matches the blood type of
the criminal given that the defendent is guilty. It is reasonable to
assume this probability is equal to 1.
Hence
the denominator is equal to 0.1*0.4 + 1*0.6 which is 0.64. Since the
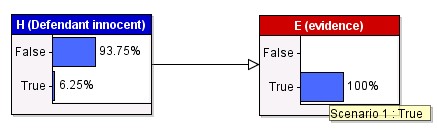
numerator was 0.04 we conclude finally that P(H | E) is equal to 0.04
divided by 0.64,
which is 0.0625.
So from our starting P(H) = 0.4, once we know the evidence we end up
with a revised belief, P(H | E), equal to 0.0625. This evidence clearly
has a significant impact.
As was already discussed here it is not necessary even for relatively simple examples like this to do any of the calculations by hand or even to remem
ber the theorem. You simply use a tool like AgenaRisk. This
involves creating two nodes as above and completing their associated
probability tables as:

|
 |
| Probability table for the node H (Defendant is inncocent) |
Probability table for node E (specifically since E has H as a parent this is the conditional probability for E|H) |
Now
the tool will automatically calculate the revised probabilities when
you enter evidence. So when you enter the evidence that E is true we
get:
Other points about Bayes Theorem
Odds version of Bayes
In some situations it is better to use the following 'odds' version of Bayes Theorem:
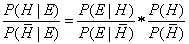
where for simplicity we have written "not H" as 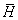
This odds version is derived by writing down the two Bayes Theorem expressions for
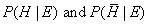
and dividing the first by the second.
In general the 'odds' in favour of an
event is just the ratio of the probability of the event happening and
the event not happening. Thus, the expression on the right hand
side of the 'odds' version of Bayes
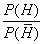
is simply the 'odds on the prior
hypothesis H' (in the above example the prior odds are 0.4/0.6 =
0.666), whereas the the expression on the left hand side
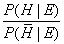
is the 'odds on the posterior hypothesis H' (that's what we want to calculate)
The other expression on the right hand side
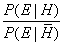
is the likelihood ratio. In our example the likelihood ratio is 0.1/1 = 0.1.
If the likelihood ratio is less than
1 then if follows that the odds on the posterior hypothesis of
innocence is less than the odds on the prior hypothesis of innocence.
Hence the evidence supports the prosecution case because the odds on
innocense have decreased (in the example the odds drop by a factor of
10 from 0.666 to 0.0666). Conversely a likelihood ratio of
greater than 1 supports the defence case since it means that the
posterior odds on innocence are greater than the prior odds.
General version of Bayes
If H has n
possible values H1, H2, ..., Hn (rather than just two "true" or
false" ) then, for any Hi the full version of Bayes Theorem
is
For an excellent web page that explains Bayes Theorem interactively try
Yuri
Yudkowsky's An Intuitive Explanation of Bayesian Reasoning
Norman
Fenton
Return to Main Page
Making Sense of Probability: Fallacies, Myths and Puzzles