The fallacy of reasoning about evidence in Court
The examples here and here
expose some classic fallacies of legal reasoning. These fallacies have,
unfortunately, often been introduced in real criminal trials.
These, and other similar fallacies of probabilistic reasoning,
would be avoided if judges, lawyers and juries were better
informed of the basics of probability theory. In fact, the entire legal
process could be simplified if those involved in the system were aware
of a simple 250-year-old theorem - Bayes Theorem - that explicitly tells us how to revise our beliefs in the light of new evidence.
For reasons that are explained below, the legal system does not
currently support using Bayes. This is, in my view, nothing short of
scandalous. In years to come our descendants will reflect in
astonishment that the single most obvious tool to help people reason
about evidence in a rational way was deliberately ignored in the very
arena where this type of reasoning is most crucial. One of the
problems about Bayes Theorem is that the mathematical and
statistical community have been really regligent in their attempts to
explain it to 'lay' people. Try googling on Bayes Theorem and you
will see what I mean.
But the explanation is quite simple and is ideally stated in a
legal context. And the mathematical formula for Bayes Theorem and
other probability laws (even though they are actually
quite straightforward) do not even need to be understood or
known because
there are tools which do all the calculations once you supply the
necessary inputs to it.
Basically we start with some hypothesis (let's call it H) which in
the legal context is usually the statement "Defendant is innocent". In
this case the hypothesis is either true or false (that is not always
the case but you do not need to assume anything else in order to
understand Bayes).
Now, people will have a belief about whether H is true or not. If you know absolutely nothing about the
defendant or the crime your belief about H will be different to that
of, say, the police officer who first charged the defendant, or the
prosecuting lawyer who has seen all of the evidence. In each of these
cases the belief will be uncertain
and so can be expressed as a probability. The police officer who first
charged the defendant might believe that H is true with a probability
of 0.1 (and hence false with a probability of 0.9), whereas you may
have no reason to believe that the defendent is any more likely to be
guilty than any other able-bodied person in the country. So, if
there are say 10 million such people, your belief will be that H is
false with a probability of 1 in 10 million) and hence that H is
true with a probability of 9,999,999 in 10 million). If there were no
witnesses to the crime then the only
person
whose belief about H is not uncertain is the defendent himself
(notwithstanding esoteric cases such as the defendant suffering amnesia
or being under a hypnotic trance). If
he really is innocent then his belief about H being true is 1
and if he is not innocent his belief about H being true is 0.
So any person must have what we call a prior belief
about H. This is their own (subjective) probability about the truth of
H at the start. So, the first key input you need to use Bayes Theorem is the answer
to the following question:
Question 1: "What is your prior belief about the probability the defendant is innocent".
(Mathematicians write this as P(H) to stand for "the probability of
H")..
What now happens is that you start to find out evidence. For every piece of evidence E you find out you will naturally want to revise your (prior) belief about H.
If the evidence 'favours' the belief that H is true (for example,
suppose the evidence is that the defendant has an alibi) then your revised belief (also
called your posterior belief)
about H being true should increase; whereas if the evidence
favours the belief that H is false (for example, a witness claims to
have seen the defendant at the scene of the crime) then your revised belief about H being false should increase.
All of that is simple common sense. The question that Bayes Theorem answers precisely is the following :
| Question 2: "what
is the revised (posterior) belief about the defendent being
inncocent given the evidence". (Mathematicians write this as P(H
| E) meaning "the probability of the hypothesis H given the evidence E") |
It turns out that, whereas answering Question 2 directly is normally difficult, it is easier to answer the following question:
| Question 3: "what is the probability of seeing the evidence given that the defendent is innocent." (Mathematicians write this as P(E | H) meaning "the probability of the evidence E given the hypothesis H" and they call it the likelihood). |
(the fact that some people wrongly think that questions 2 and 3 really are the same is exactly the prosecution fallacy)
Pictorially we can represent the situation for Question 3 as:
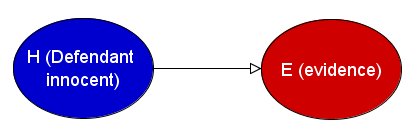
Suppose, for example, the evidence is
"a blood sample of the criminal found at the
scene matches the blood type of the defendent". If that blood type
is
found in 1 in every 10 people, then the answer to question 3 is
simply 0.1. Once we have an answer to Questions 1 and 3 then we have
all we need to use Bayes Theorem. (the fact that you do
not actually need to know Bayes Theorem in order to 'use it' and
appreciate the result is emphasized here by giving you a separate
link to the theorem itself). So suppose that your
answer to Question 1 is 0.4. Then, using one of many Bayesian
calculation tools that allow you to answer these questions (here we are
using AgenaRisk) you will see the following result:
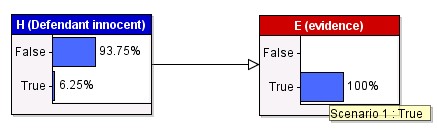
So,
having observed the evidence is true (namely that the blood type
matches the defendant's), with the answers to Questions 1 and 3 as above
the revised belief that the defendant is innocent drops to 0.0625 (i.e.
6.25%). In other words the answer to Question 2 is 0.0625 and this answer is automatically calculated (using Bayes Theorem). Anybody who arrives at a different answer with these same assumptions is demonstrably irrational.
It is also worth noting that the answers to questions 1 and 3 are also used by Bayes Theorem to make the following calculations:
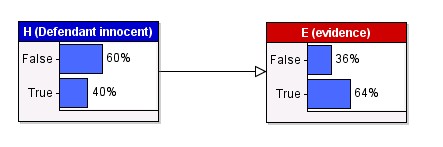
This is what mathematicians call the 'marginal' probabilities. For H
the marginal probability is just the prior probability, but for E the
marginal is the probability of the evidence before we have seen any.
So, even before seeing evidence about the blood, there is a 0.64
probability that the blood type would match the defendant's. Many
jurors would be surprised at how high the probability is in the case.
In fact most lay people assume the probability is 0.1 because they
fall into the trap of the base rate fallacy,
whereby they think of the (unconditional) probability of seeing the
evidence (in this case a random person having the matching blood type)
and they ignore the prior probability of inncocence.
I
stress that you can see the details of how the calculations work here,
but lawyers and jurors for example should never have to know any of
that. They simply have to answer questions 1 and 3 and trust a Bayesian
tool to do the calculations. In fact, since normally the answer to
Question 3 would be provided by a subject expert (such as a DNA expert)
this should make the job of the jury even easier still.
So what are the objections to this approach in the legal system?
There are two objections. One rational and one irrational.
The irrational objection concerns the calculation of the answer to
Question 2. According to the British legal system, finding the answer
to Question 2 must
be left to the individual jurors and it is a matter for them
(and only them) as to how they arrive at a conclusion. In other words once
they have their answers to questions 1 and 3 they must work out for
themselves the answer to question 2. Nobody forbids them from
using Bayes
theorem but, given their likely ignorance of
the theorem, they will almost certainly come to a conclusion that is
computationally wrong. That is because, whereas Bayes
theorem provides the only rational answer to the
question, people who do not 'apply' the theorem consistently
and demonstrably
arrive at incorrect answers for their given assumptions about questions
1 and 3. Given the established and (mathematically) universally agreed
pedigree of Bayes Theorem, how is it possible that the legal system
arrived at the situation whereby it is ignored? Sadly, it is because on
the rare occasions where Bayes has been introduced into court, experts
have attempted to explain the calculations from first principles rather
than simply presenting the results of the calucations as above. In
doing so they confused the jury, judge and lawyers. A reasonable
analogy to this situation would be the following:
An expert in court presents the result of dividing 38659 by 27104
as 1.42632. He is asked how he arrived at this figure. Instead of
simply saying he used a calculator (and demonstrating the use of the
calculator to check that he entered the numbers correctly) he attempts
to explain the calculation in terms of the sequence of binary
arithmetic functions taking place at the hardware circuit level.
If an expert really
did this then he would also inevitably confuse the jury. But you
would conclude that what the expert did was unnecessary. You
would surely not reject the use
of calculators to perform long division on the basis that it is too
difficult for lay people to understand the underlying sequence of actions that take
place at the hardware circuit level. Yet this is exactly what has happened in the case of Bayes Theorem.
The more rational objection to Bayes (though
interstingly less prominently articulated within the legal profession)
comes from the crucial dependence on the subjective prior belief about
H. It is obvious that people with
vastly different 'prior' beliefs about H will (even using Bayes
Theorem) end up with different revised beliefs when they are both
presented with the same piece of evidence. This observation underpins
the legal view that Bayes in 'inappropriate'. But even in this case the
legal sensitivities are somewhat spurious. For a start, jurors will
(whether they are asked explicitly or not) have their own prior beliefs
about innocence. Just because there is disagreement about the
'starting'
position this does not justfify rejecting the only rational way to
reason from that starting position. Moreover, if the evidence clearly
favours one outcome then (if Bayes is applied) any two revised
beliefs will certainly be closer than the corresponding two prior
beliefs. And if the two
people are subsequently presented with another piece of evidence then
their revised beliefs will get closer still. In fact, the more (common)
evidence they see the more their beliefs will converge. With enough
consistent evidence the priors become almost irrelevant. That does not
help
us in the case where there may be few pieces of truly convincing
evidence, but it nevertheless is an important counter to those who
reject Bayes on the grounds that it is 'all too dependent
on subjective priors'.
For more information on
fallacies in legal reasoning read this article:
Fenton NE and Neil M,
''The Jury
Observation Fallacy and the use of Bayesian Networks to present
Probabilistic Legal Arguments'', Mathematics Today ( Bulletin of the
IMA, 36(6)), 180-187, 2000.
which is available here:
http://www.agenarisk.com/resources/white_papers/jury_fallacy_revised.pdf
These (and related) issues also arise in the case of Shirley McKie. For an excellent account of this see Steve Horn's dedicated web pages.
Here is the material on Bayes Theorem itself..
For an excellent web page that explains Bayes Theorem interactively try Yuri Yudkowsky's An Intuitive Explanation of Bayesian Reasoning
Norman
Fenton
Return to Main Page
Making Sense of Probability: Fallacies, Myths and Puzzles