True Bayesians actually consider conditional probabilities as more basic than joint probabilities . It is easy to define P(A|B) without reference to the joint probability P(A,B). To see this note that we can rearrange the conditional probability formula to get:
P(A|B) P(B) = P(A,B)
but by symmetry we can also get:
P(B|A) P(A) = P(A,B)
It follows that:
![]()
which is the so-called Bayes Rule.
It is common to think of Bayes rule in terms of updating our belief about a hypothesis A in the light of new evidence B. Specifically, our posterior belief P(A|B) is calculated by multiplying our prior belief P(A) by the likelihood P(B|A) that B will occur if A is true.
The power of Bayes' rule is that in many situations where we want to compute P(A|B) it turns out that it is difficult to do so directly, yet we might have direct information about P(B|A). Bayes' rule enables us to compute P(A|B) in terms of P(B|A).
For example, suppose that we are interested in diagnosing cancer in patients who visit a chest clinic.
Let A represent the event "Person has cancer"
Let B represent the event "Person is a smoker"
We know the probability of the prior event P(A)=0.1 on the basis of past data (10% of patients entering the clinic turn out to have cancer). We want to compute the probability of the posterior event P(A|B). It is difficult to find this out directly. However, we are likely to know P(B) by considering the percentage of patients who smoke – suppose P(B)=0.5. We are also likely to know P(B|A) by checking from our record the proportion of smokers among those diagnosed. Suppose P(B|A)=0.8.
We can now use Bayes' rule to compute:
P(A|B) = (0.8 ´ 0.1)/0.5 = 0.16
Thus, in the light of evidence that the person is a smoker we revise our prior probability from 0.1 to a posterior probability of 0.16. This is a significance increase, but it is still unlikely that the person has cancer.
The denominator P(B) in the equation is a normalising constant which can be computed, for example, by marginalisation whereby
![]()
Hence we can state Bayes rule in another way as:
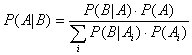
See an example of Bayes' theorem