In the introduction to Bayesian probability we explained that the notion of degree of belief in an uncertain event A was conditional on a body of knowledge K. Thus, the basic expressions about uncertainty in the Bayesian approach are statements about conditional probabilities. This is why we used the notation P(A|K) which should only be simplified to P(A) if K is constant. Any statement about P(A) is always conditioned on a context K
In general we write P(A|B) to represent a belief in A under the assumption that B is known. Even this is, strictly speaking, shorthand for the expression P(A|B,K) where K represents all other relevant information. Only when all such other information is irrelevant can we really write P(A|B).
The traditional approach to defining conditional probabilities is via joint probabilities. Specifically we have the well known 'formula':
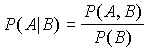
This should be really be thought of as an axiom of probability. Just as we saw the three probability axioms were 'true' for frequentist probabilities , so this axiom can be similarly justified in terms of frequencies:
Example: Let A denote the event 'student is female' and let B denote the event 'student is Chinese'. In a class of 100 students suppose 40 are Chinese, and suppose that 10 of the Chinese students are females. Then clearly, if P stands for the frequency interpretation of probability we have:
P(A,B) = 10/100 (10 out of 100 students are both Chinese and female)
P(B) = 40/100 (40 out of the 100 students are Chinese)
P(A|B) = 10/40 (10 out of the 40 Chinese students are female)
It follows that the formula for conditional probability 'holds'.
In those cases
where P(A|B) = P(A) we say that A and B are independent.
If P(A|B,C) =
P(A|C) we say that A and B are conditionally
independent
given C.
For a full
discussion of these important notions see here
and also the section on transmitting
evidence in BBNs.