Why clever people cannot understand Bayes Theorem and what you can do about it (show an event tree)
The following is a classic problem that is easily solved by Bayes Theorem (it is the same problem we posed here).
"One
in a thousand people has a prevalence for a particular heart disease.
There is a test to detect this disease. The test is 100%
accurate
for people who have the disease and is 95% accurate for those who don't
(this means that 5% of people who do not have the disease will be
wrongly diagnosed as having it).
If a randomly selected person tests positive what is the probability
that the person actually has the disease?"
The usual solution using the Bayes formula is given here (at the bottom of the page).
But there is a problem. Most people (including very clever ones
like doctors and lawyers) cannot understand or follow the solution when
presented in the normal 'formulaic' way. There are a number of reasons
for this. Fear of mathematics is one and another is the inability of
most people to understand abstract probabilities. For example, for the
Bayes theorem solution you start with the prior probability of a person
having the disease being equal 0.001. But most people have
trouble understanding what a probability of 0.001 means and how, for
example it differs from a probability of 0.0001. There are high court
judges and top surgeons who would not understand that an event with
probability of 0.001 is 10 times more likely than an event with
probability 0.0001. But what people do
understand is that if there is a one in a thousand chance of a person
having the disease then in a set of 100,000 people about 100 will have
the disease. So the simple trick to improve understanding is to use
whole numbers in a contextualised set of people (rather than abstract
probabilities) . Then you can present the equivalent of the Bayesian
argument mechanically (using what is called an event/decision tree)
like this:
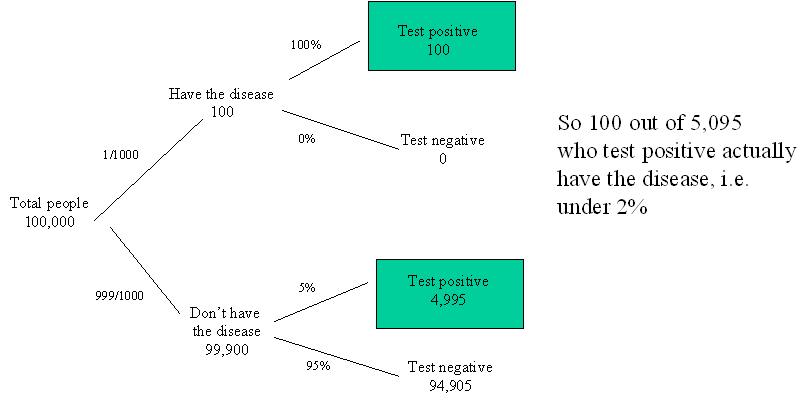
What we have done here is consider
the different alternatives (as in the formulaic approach), but in a way
that makes it absolutely clear how we arrive at the correct posterior
probability. You can think of this as a formal version of this animation.
