Why are you more likely to die in a car crash when the road conditions are good compared with when they are bad?

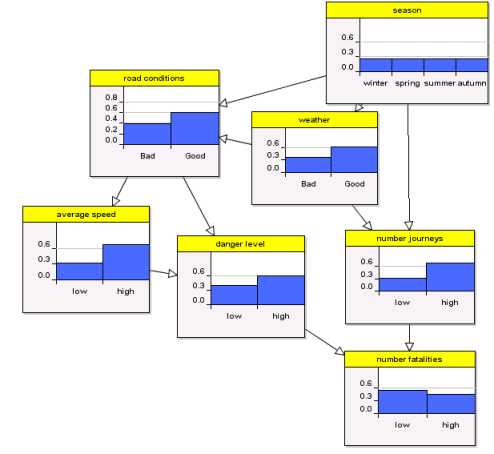
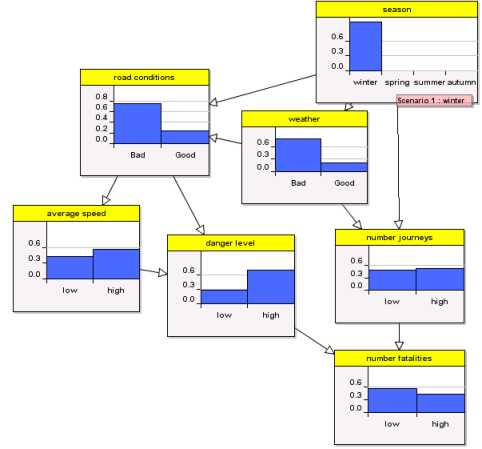
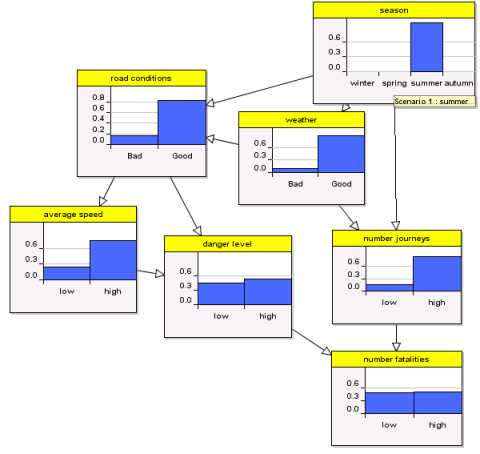
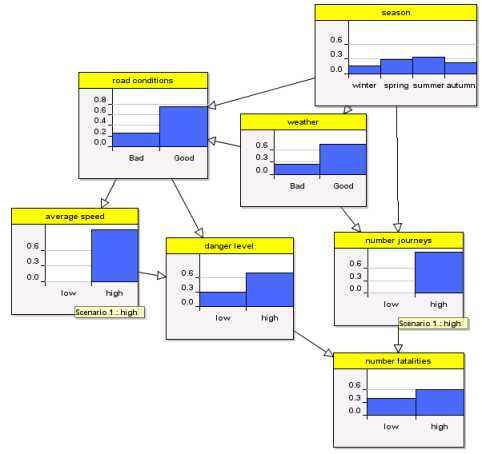
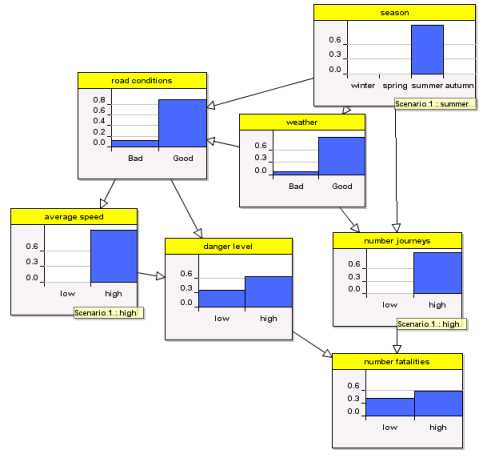
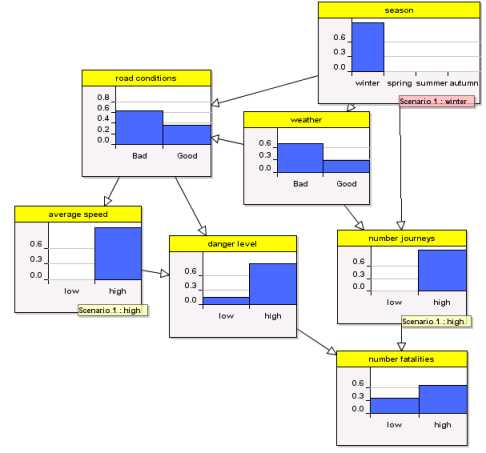
The data for road fatalaties in both the US and Europe is very curious. The month in which there are fewest fatalities is February followed by January. In other words, there are fewest fatalities when the weather is at its worst and when presumably the roads are at their most dangerous. If you apply traditional statistical regression techniques using this available data you will end up with a simple model like THIS:

car0

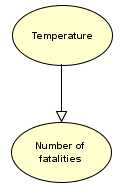
Colder months yield fewer fatalities. Now as a purely predictive model you could argue that this is not too bad. But for risk management it is useless, because it provides no explanatory power at all. In fact, from a risk perspective this model would provide totally irrational information since it would suggest that if you want to minimise your probability of dying in a car crash you should do your driving when the roads are at their most dangerous.

What we know is that there are a number of causal factors which do much to explain the apparently strange statistical observations.

Clearly the season influences whether the weather is good or not, and both this and the season influence whether road conditions are good.
When the road conditions are bad people tend to drive slower.
The danger level is at its highest when people are driving fast and the road conditions are bad.
Both the season and the weather influence the number of journeys made - people generally make more journeys in summer and will generally drive less when wearther conditions are bad.
The actual number of fatalities is influenced not just by the danger level but by the number of journeys. If relatively few people are driving, albeit dangerously, there will be relatively few fatalities.

Using this kind of model, which happens to be an example of Bayesian Network, we can not just fully explain the statistical observations but also use it to make sensible decisions about risk.

Notice that with each variable are the probabilities.

car2

At this point we haven't entered any observations in the model, so what we have above are called the prior probabilities. For example, the prior probability that the weather is good is 63% and all the seasons have equal probabilities. The prior probability of high number of fatal accidents is 46%.
Now let’s enter some observations. Let’s first see what happens in winter.

car3

Notice how all the probabilities change. In winter road conditions are more likely to be bad, but this means that people tend to drive slower. Also fewer journeys are made in winter. The impact of this is that the probability of high number of fatal accidents has dropped to 43%.
Now compare what happens in summer.

car4

Road conditions are better but this means people drive faster. There are also more journeys. These factors explain why we now see an increase in the probability of high fatalities to 50%. This explains the strange statistical results but doesn't help us with risk reduction.

The only things we directly control ourselves are the speed we drive and the number of journeys we make. Let’s suppose that, irrespective of the time of year, we all drive fast and make a lot of journeys:

car5

Notice how the probability of fatalities increases again to 61%.
However, now compare the situation between summer and winter. In summer the road conditions are less likely to be bad so we see a drop to 59% in high fatalitiy prob. In winter road conditions are worse and the probability increases to 65%.


Driving fast and often (Summer)	Driving fast and often Winter

This tells us that if we do not alter our driving habits then fatalities are more likely in winter than summer - exactly the opposite of what the naïve model was telling us.

You can run the above model by downloading AgenaRisk and opening the model here.