BBNs make explicit the dependencies between different variables. In general there may be relatively few direct dependencies (modelled by arcs between nodes of the network) and this means that many of the variables are conditionally independent . In the simple example above the nodes 'Norman late' and 'Martin late' are conditionally independent (there is no arc linking them); once the value of 'train strike' is known knowledge of 'Norman late' does not effect the probability of 'Martin late' and vice versa.
The existence of unlinked (conditionally independent) nodes in a network drastically reduces the computations necessary to work out all the probabilities we require. In general, all the probabilities can be computed from the joint probability distribution . Crucially, this joint probability distribution is far simpler to compute when there are conditionally independent nodes.
Suppose, for example, that we have a network consisting of five variables (nodes) A,B,C,D,E. If we do not specify the dependencies explicitly then we are essentially assuming that all the variables are dependent on eachother. The chain rule enables us to calculate the joint probability distribution p(A,B,C,D,E) as:
p(A,B,C,D,E) = p(A|B,C,D,E)*p(B|C,D,E)*p(C|D,E)*p(D|E)*p(E)
However, suppose that the dependencies are explicitly modelled in a BBN as:
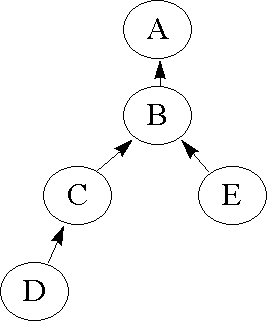
Then the joint probability distribution p(A,B,C,D,E) is much simplified:
p(A,B,C,D,E) = p(A|B)*p(B|C,E)*p(C|D)*p(D)*p(E)
To see the general case click here.