Consider the BBN in the figure below.
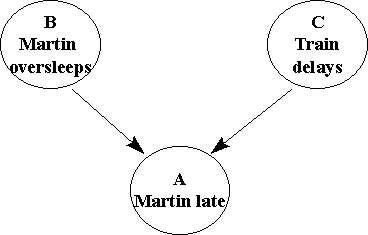
Clearly any evidence about B or C is transmitted to A. However, we are now concerned about whether evidence can be transmitted between B and C.
If we have no information about whether or not Martin is late, then clearly whether or not Martin oversleeps and whether or not there are train delays are independent. In other words if nothing is known about A then A's parents (B and C) are independent, so no evidence is transmitted between them.
However, if anything is known about A (even so-called soft evidence ) then the parents of A become dependent. For example, suppose that Martin usually hangs up his coat in the hall as soon as he gets in to work. Then if we observe that Martin's coat is not hung up after 9.00am our belief that he is late increases (note that we do not know for certain that he is late - we have soft as opposed to hard evidence - because on some days Martin does not wear a coat). Even this 'soft' evidence about Martin being late increases our belief in both B:Martin oversleeping and C:Train delays (see also the principle of 'explaining away' ). We say that B and C are conditionally dependent (on A).
It follows that in a converging connection evidence can only be transmitted between the parents B and C when the converging node A has received some evidence (which can be soft or hard).