[papers/_private/small_logo.html][papers/_private/horizontal_navbar.html]
What you can and cannot do with the basic metrics In this section we will look at recent empirical work which explains the limitations of the basic measures and explains in particular problems with the so-called complexity metrics. We restrict our attention to the use of metrics for quality control, assessment and prediction. Specifically, in what follows we will examine what you can and cannot do with defect metrics and size and complexity metrics. We assume that readers already acknowledge the need to distinguish between:
- defects which are discovered at different life-cycle phases. Most notably defects discovered in operation (we call these failures) must always be distinguished from defects discovered during development (which we refer to as faults since they may lead to failures in operation).
- different categories of defects (including defects with different levels of criticality)
Ultimately one of the major objectives of software metrics research has been to produce metrics which are good ‘early’ predictors of reliability (the frequency of operational defects). It is known that stochastic reliability growth models can produce accurate predictions of the reliability of a software system providing that a reasonable amount of failure data can be collected for that system in representative operational use [Brocklehurst and Littlewood 1992]. Unfortunately, this is of little help in those many circumstances when we need to make predictions before the software is operational. In [Fenton and Neil 1998] we reviewed the many studies advocating statistical models and metrics to address this problem. Our opinion of this work is not high - we found that many methodological and theoretical mistakes have been made. Studies suffered from a variety of flaws ranging from model mis-specification to use of inappropriate data. We concluded that the existing models are incapable of predicting defects accurately using size and complexity metrics alone. Furthermore, these models offer no coherent explanation of how defect introduction and detection variables affect defect counts.
In [Fenton and Ohlsson 1998] we used case study data from two releases of a major commercial system to test a number of popular hypotheses about the basic metrics. The system was divided into many hundreds of modules. The basic metrics data were collected at the module level (the metrics were: defects found at four different testing phases, including in operation, LOC, and a number of complexity metrics including cyclomatic complexity). We were especially interested in hypotheses which lie at the root of the popularity for the basic metrics. Many of these are based around the idea that a small number of the modules inevitably have a disproportionate number of the defects; the assumption is then that metrics can help us to identify early in the development cycle such fault and failure prone modules.
The hypotheses and results are summarised in Table 1. We make no claims about the generalisation of these results. However, given the rigour and extensiveness of the data-collection and also the strength of some of the observations, we feel that there are lessons to be learned by the wider community.
Number
Hypothesis
Case study evidence?
- a
a small number of modules contain most of the faults discovered during pre-release testing
Yes - evidence of 20-60 rule
- b
if a small number of modules contain most of the faults discovered during pre-release testing then this is simply because those modules constitute most of the code size
No
2.a
a small number of modules contain most of the operational faults
Yes - evidence of 20-80 rule
2.b
if a small number of modules contain most of the operational faults then this is simply because those modules constitute most of the code size
No - strong evidence of a converse hypothesis
Modules with higher incidence of faults in early pre-release likely to have higher incidence of faults in system testing
Weak support
Modules with higher incidence of faults in all pre-release testing likely to have higher incidence of faults in post-release operation
No - strongly rejected
- a
Smaller modules are less likely to be failure prone than larger ones
No
5b
Size metrics (such as LOC) are good predictors of number of pre-release faults in a module
Weak support
5c
Size metrics (such as LOC) are good predictors of number of post-release faults in a module
No
5d
Size metrics (such as LOC) are good predictors of a module’s (pre-release) fault-density
No
5e
Size metrics (such as LOC) are good predictors of a module’s (post-release) fault-density
No
Complexity metrics are better predictors than simple size metrics of fault and failure-prone modules
No ( for cyclomatic complexity), but some weak support for metrics based on SigFF
Fault densities at corresponding phases of testing and operation remain roughly constant between subsequent major releases of a software system
Yes
Software systems produced in similar environments have broadly similar fault densities at similar testing and operational phases
Yes
Table 1: Support for the hypotheses provided in this case study
The evidence we found in support of the two Pareto principles 1a) and 2a) is the least surprising, but there was previously little published empirical data to support it. However, the popularly believed explanations for these two phenomena were not supported in this case:
- It is not the case that size explains in any significant way the number of faults. Many people seem to believe (hypotheses 1b and 2b) that the reason why a small proportion of modules account for most faults is simply because those fault-prone modules are disproportionately large and therefore account for most of the system size. We have shown this assumption to be false for this system.
- Nor is it the case that ‘complexity’ (or at least complexity as measured by ‘complexity metrics’) explains the fault-prone behaviour (hypothesis 6). In fact complexity is not significantly better at predicting fault and failure prone modules than simple size measures.
- It is also not the case that the set of modules which are especially fault-prone pre-release are going to be roughly the same set of modules that are especially fault-prone post-release (hypothesis 4).
The result for hypothesis 4 is especially devastating for much software metrics work. The rationale behind hypothesis 4 is the belief in the inevitability of ‘rogue modules’ - a relatively small proportion of modules in a system that account for most of the faults and which are likely to be fault-prone both pre- and post release. It is often assumed that such modules are somehow intrinsically complex, or generally poorly built. This also provides the rationale for complexity metrics. For example, Munson and Khosghoftaar asserted:
‘There is a clear intuitive basis for believing that complex programs have more faults in them than simple programs’, [Munson and Khosghoftaar, 1992]
Not only was there no evidence to support hypothesis 4, but there was evidence to support a converse hypothesis. In both releases almost all of the faults discovered in pre-release testing appear in modules which subsequently revealed almost no operation faults (see Figure 1)
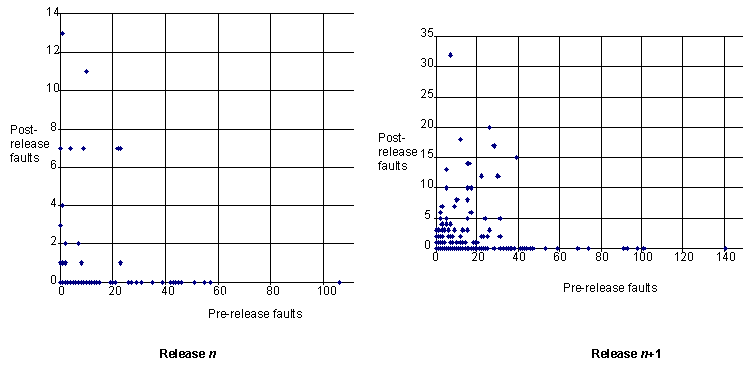
Figure 1: Scatter plot of pre-release faults against post-release faults for successive versions of a major system (each dot represents a module selected randomly)
These remarkable results are also closely related to the empirical phenomenon observed by Adams [Adams 1984]—that most operational system failures are caused by a small proportion of the latent faults. The results have major ramifications for the commonly used fault density metric as a de-facto measure of user perceived software quality. If fault density is measured in terms of pre-release faults (as is common), then at the module level this measure tells us worse than nothing about the quality of the module; a high value is more likely to be an indicator of extensive testing than of poor quality. Modules with high fault density pre-release are likely to have low fault-density post-release, and vice versa. The results of hypothesis 4 also bring into question the entire rationale for the way software complexity metrics are used and validated. The ultimate aim of complexity metrics is to predict modules which are fault-prone post-release. Yet, most previous ‘validation’ studies of complexity metrics have deemed a metric ‘valid’ if it correlates with the (pre-release) fault density. Our results suggest that ‘valid’ metrics may therefore be inherently poor at predicting what they are supposed to predict.
What we did confirm was that complexity metrics are closely correlated to size metrics like LOC. While LOC (and hence also the complexity metrics) are reasonable predictors of absolute number of faults, they are very poor predictors of fault density.
To go back to our resources section click here.
[papers/_private/copyright_notice.html]
Last modified: July 28, 1999.