Please note: This page is no longer being maintained. An updated tutorial on this subject can be found here.
This section is a brief self-contained overview of Bayesian nets. For a full description and tutorial see the BBN tutorial section.
A Bayesian belief net (BBN) is a directed graph, together with an associated set of probability tables. The graph consists of nodes and arcs as shown below. The nodes represent variables, which can be discrete or continuous. For example, the node 'faults in test/review' is discrete having values 0,1,2,.., whereas the node 'system safety' might be continuous (such as the probability of failure on demand). The arcs represent causal/influential relationships between variables. For example, the number of faults in test/review is influenced by the correctness of the solution and the accuracy of testing, hence we model this relationship by drawing appropriate arcs as shown.
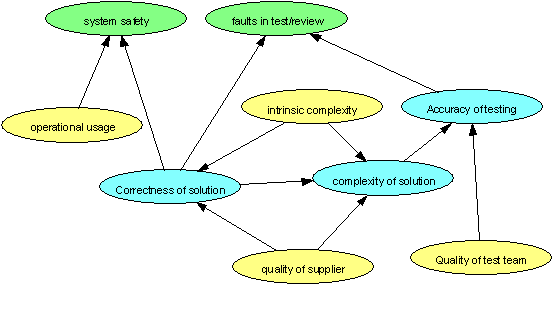
System safety assessment BBN example
The key feature of BBNs is that they enable us to model and reason about uncertainty. The BBN forces the assessor to expose all assumptions about the impact of different forms of evidence and hence provides a visible and auditable dependability or safety argument.
Consider the example above. Suppose we knew that the correctness of the solution was 'low' and the accuracy of testing is 'high'. Then the probability of finding a high number of faults in test would be more than if we knew the correctness of the solution was 'high' and the accuracy of testing is 'low'. In the BBN we model this kind of dependence between uncertain variables by filling in a node probability table (NPT). Thus, for the node 'faults in test/review' the NPT might look like that shown in the table below. The NPTs capture the conditional probabilities of a node given the state of its parent nodes.
NPT for 'faults found in inspection/testing'

BBNs are a way of describing complex probabilistic reasoning. The advantage of describing a probabilistic argument via a BBN, compared to describing it via mathematical formulas and prose, is that the BBN represents the structure of the argument in an intuitive, graphical format. The main use of BBNs is in situations that require statistical inference — in addition to statements about the probabilities of events, the user knows some evidence, that is, some events that have actually been observed, and wishes to infer the probabilities of other events, which have not as yet been observed. Using probability calculus and Bayes theorem it is then possible to update the values of all the other probabilities in the BBN. This is called propagation). Bayesian analysis can be used for both 'forward' and 'backward' inference.
For example, suppose we know that the quality of the supplier is 'low' and the intrinsic complexity of the problem is 'high'. Then if we enter these facts and propagate their effects through the BBN it will update all of the other probabilities, giving for example a revised value for the probability of system safety. The figure below shows the actual results of entering different types of evidence (evidence is shown as a red bar).
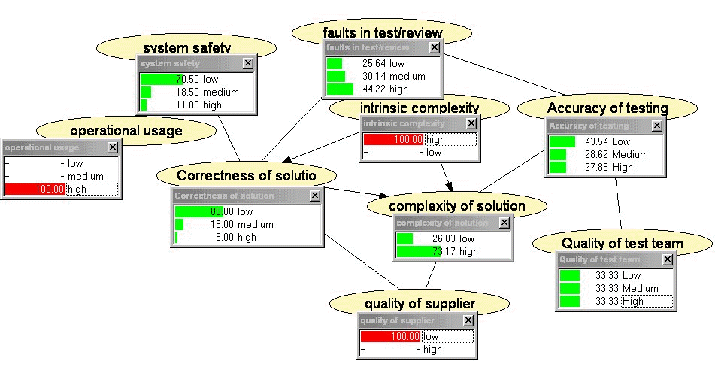
Propagating evidence in the system safety assessment BBN example
Although Bayesian probability been around for a long time it is only in the last few years that efficient algorithms (and tools to implement them) have been developed to enable propagation in networks with a reasonable number of variables. The Bayesian propagation computations shown above, even for an example as small as this, are very complex and cannot be calculate manually. Here we have used the Hugin tool, that implements the breakthrough propagation algorithm of Lauritzen and Spiegelhalter. A more modern and powerful BBN tool is the AgenaRisk tool. With this tool it is possible to perform fast propagation in large BBNs (with hundreds of nodes and millions of state combinations. The recent explosion of interest in BBNs is due to these developments which mean that for the first time realistic size problems can be solved. These recent developments, in our view, make BBNs the best method for reasoning about uncertainty. To date BBNs have proven useful in applications such as medical diagnosis and diagnosis of mechanical failures. Their most celebrated use has been by Microsoft - BBNs underlie the help wizards in Microsoft Office and also underlie the interactive printer fault diagnostic system on the Microsoft web site.