The conditional probability of A given B is represented by P(A|B). The variables A and B are said to be independent if P(A)= P(A|B) (or alternatively if P(A,B)=P(A) P(B) because of the formula for conditional probability ).
Example1 Suppose Norman and Martin each toss separate coins. Let A represent the variable "Norman's toss outcome", and B represent the variable "Martin's toss outcome". Both A and B have two possible values (Heads and Tails). It would be uncontroversial to assume that A and B are independent. Evidence about B will not change our belief in A.
Example2 Now suppose both Martin and Norman toss the same coin. Again let A represent the variable "Norman's toss outcome", and B represent the variable "Martin's toss outcome". Assume also that there is a possibility that the coin in biased towards heads but we do not know this for certain. In this case A and B are not independent. For example, observing that B is Heads causes us to increase our belief in A being Heads (in other words P(a|b)>P(b) in the case when a=Heads and b=Heads).
In Example 2 the variables A and B are both dependent on a separate variable C, "the coin is biased towards Heads" (which has the values True or False). Although A and B are not independent, it turns out that once we know for certain the value of C then any evidence about B cannot change our belief about A. Specifically:
P(A|C) = P(A|B,C)
In such case we say that A and B are conditionally independent given C.
In many real life situations variables which are believed to be independent are actually only independent conditional on some other variable.
Example 3 Suppose that Norman and Martin live on opposite sides of the City and come to work by completely different means, say Norman comes by train while Martin drives. Let A represent the variable "Norman late" (which has values true or false) and similarly let B represent the variable "Martin late". It would be tempting in these circumstances to assume that A and B must be independent. However, even if Norman and Martin lived and worked in different countries there may be factors (such as an international fuel shortage) which could mean that A and B are not independent. In practice any model of uncertainty should take account of all reasonable factors. Thus while, say, a meteorite hitting the Earth might be reasonably excluded it does not seem reasonable to exclude the fact that both A and B may be affected by a Train strike (C). Clearly P(A) will increase if C is true; but P(B) will also increase because of extra traffic on the roads. Thus the situation is represented in the following animation (which is actually a BBN)
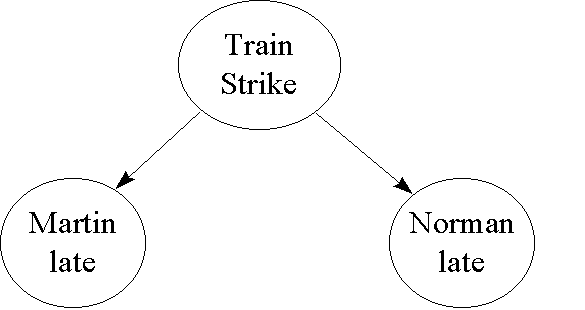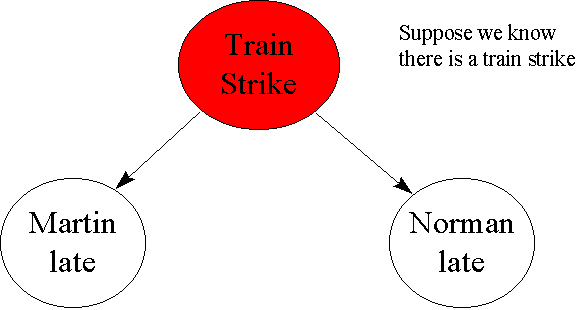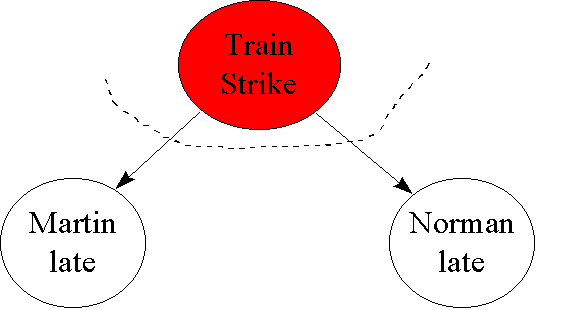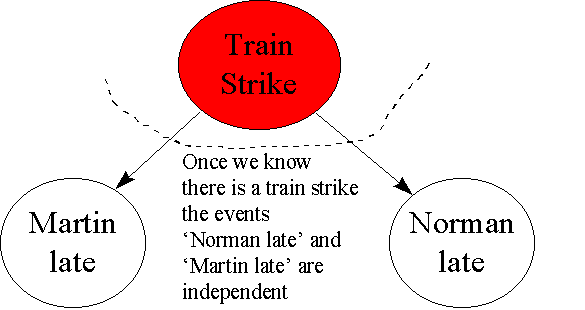
Now, "Martin late" and "Norman late" are conditionally independent given "Train strike":
See also the section on transmitting evidence in BBNs.