Consider the following BBN:
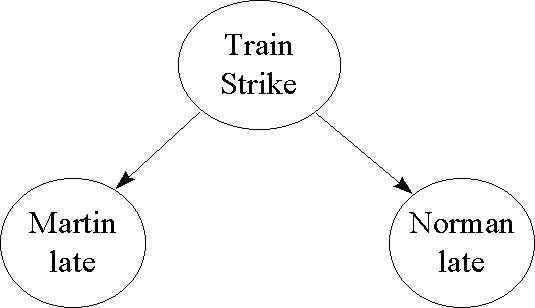
Let A denote 'Train strike', B denote 'Martin late' and C denote 'Norman late'.
Any evidence about A is transmitted to both B and C. For example, if we have evidence which increases our belief in a train strike (A) then this in turn will increase our belief in both Martin being late (B) and Norman being late (C).
Of more interest is whether information about B can be transmitted to C (and vice versa). Suppose we have no hard evidence about A (that is, we do not know for certain whether or not there is a train strike). If we have some evidence that Martin is late (B) then this increases our belief in A (that is, we also reason in the opposite direction of the causal arrows). This in turn increases our belief in C. In other words, evidence about B (Martin late) is transmitted through to C (Norman late).
However, suppose now that we have hard evidence about A, that is we know for certain whether or not there is a train strike (we also say that A is instantiated). In this case any evidence about B (Martin late) does not change in any way our belief about C (Norman late); this is because the certainty of A blocks the evidence from being transmitted (it becomes irrelevant once we know A for certain). The value of C is only influenced by the certainty of A. Thus, when A is known for certain B and C become independent.
Because the independence of B and C is conditional on the certainty of A, we say formally that B and C are conditionally independent (given A). (For a more basic explanation of independence and conditional independence click here ).
In summary: evidence can be transmitted from B to C through a diverging connection A unless A is instantiated. We say that B and C are d-separated given A.
For an animation in the general case click here